pytagi.nn.activation#
Classes#
Applies the Rectified Linear Unit function. |
|
Applies the Sigmoid function element-wise. |
|
Applies the Hyperbolic Tangent function. |
|
Applies a probabilistic Rectified Linear Unit approximation. |
|
Applies a probabilistic picewise-linear Sigmoid-like function. |
|
Applies a probabilistic piecewise-linear Hyperbolic Tangent function. |
|
Applies the Softplus function element-wise. |
|
Applies the Leaky Rectified Linear Unit function element-wise. |
|
Applies a Local-Linearization of the Softmax function to an n-dimensional input. |
|
Applies the EvenExp activation function. |
|
Applies a probabilistic Remax approximation function. |
|
Applies a probabilistic Softmax approximation function. |
Module Contents#
- class pytagi.nn.activation.ReLU[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies the Rectified Linear Unit function.
This layer processes an input Gaussian distribution and outputs the moments for a rectified linear unit. This layer relies on a first-order Taylor-series approximation where the activation function is locally linearized at the input expected value.
\[\text{ReLU}(x) = (x)^+ = \max(0, x)\]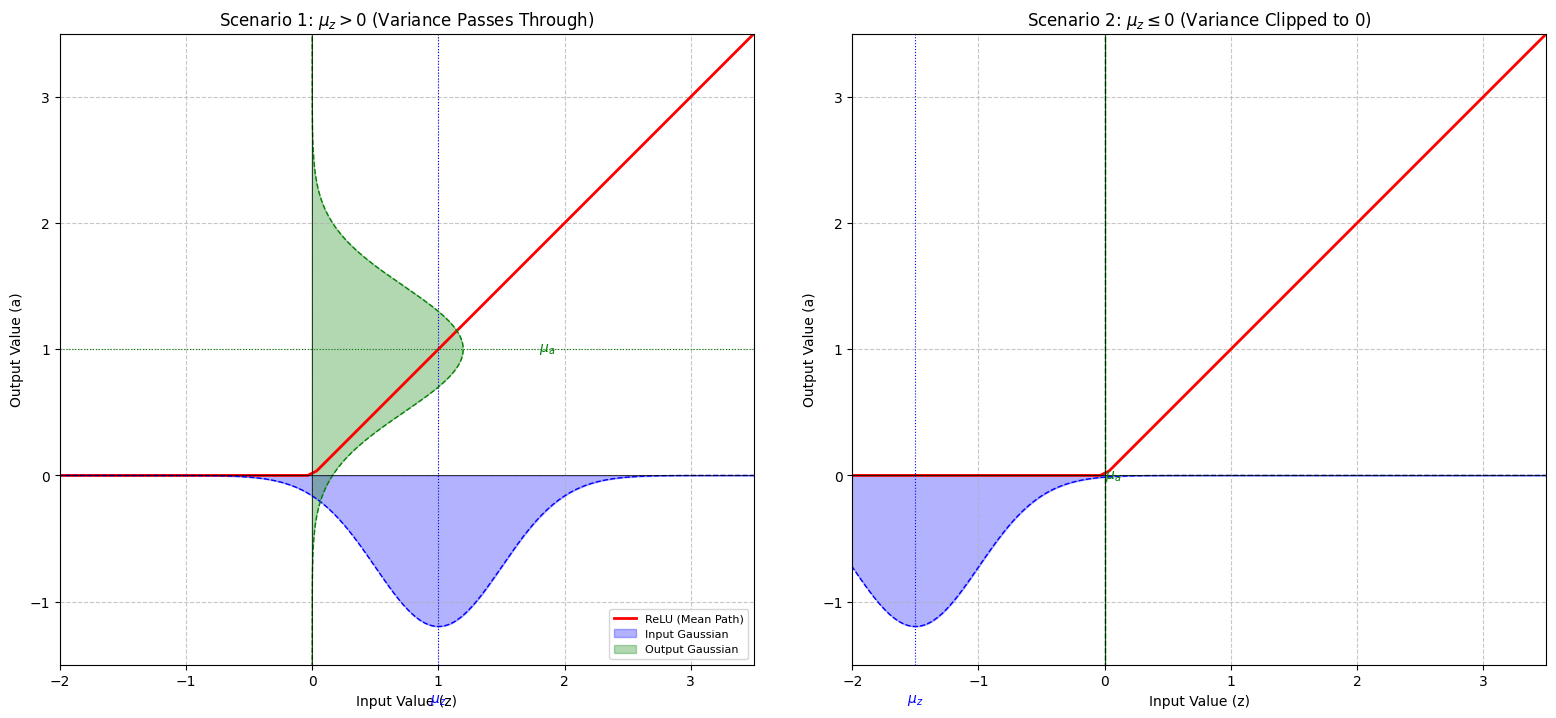
Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.Sigmoid[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies the Sigmoid function element-wise.
This layer approximates the moments after applying the sigmoid function whose values are constrained to the range (0, 1). This layer relies on a first-order Taylor-series approximation where the activation function is locally linearized at the input expected value.
\[\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + e^{-x}}\]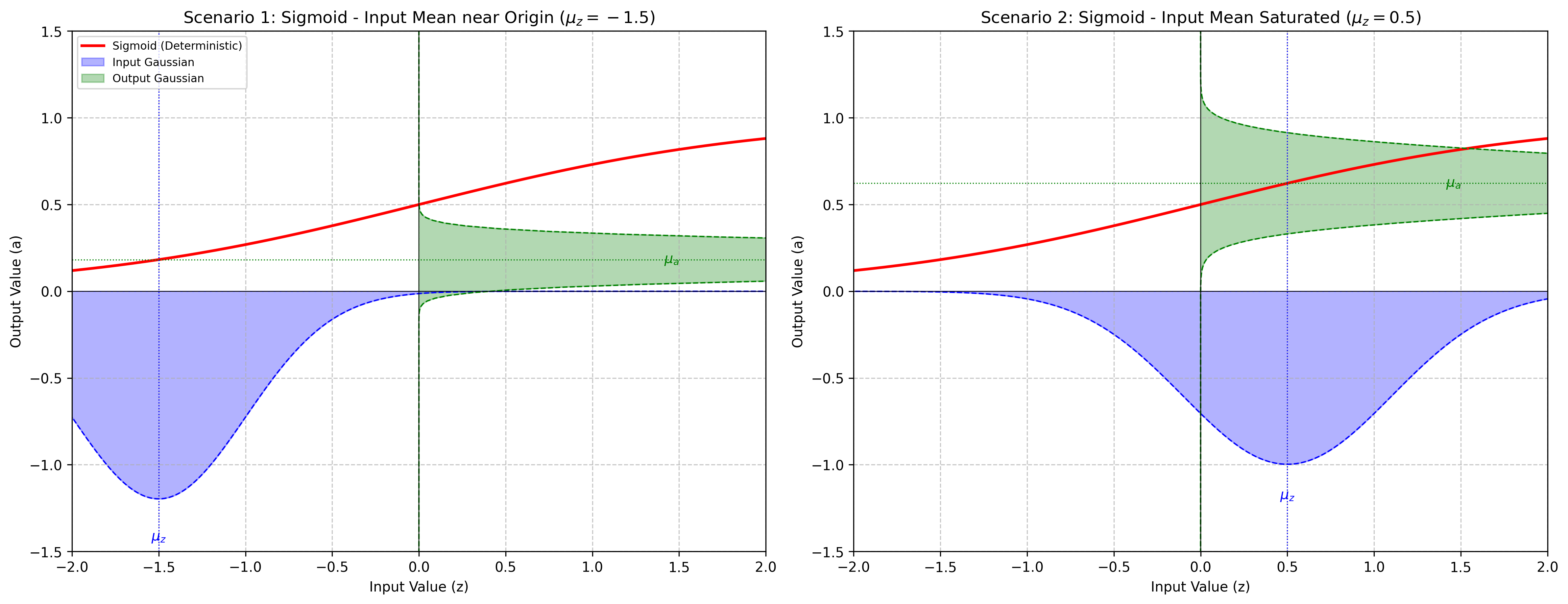
Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.Tanh[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies the Hyperbolic Tangent function.
This layer approximates the moments after applying the Tanh function whose values are constrained to the range (-1, 1). This layer relies on a first-order Taylor-series approximation where the activation function is locally linearized at the input expected value.
\[\text{Tanh}(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]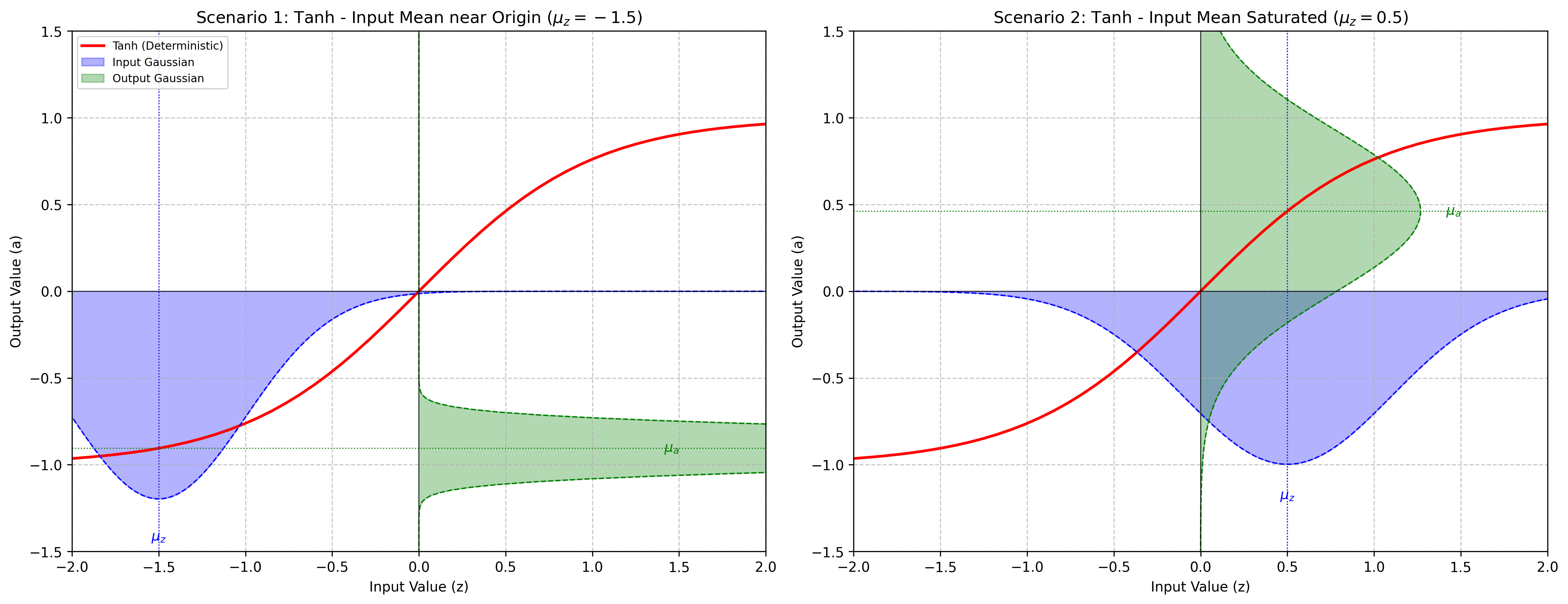
Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.MixtureReLU[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies a probabilistic Rectified Linear Unit approximation.
This layer processes an input Gaussian distribution and outputs the moments for a rectified linear unit. This layer relies on exact moment calculations.
For an input random variable \(X \sim \mathcal{N}(\mu, \sigma^2)\), the output \(Y = \max(0, X)\) results in a rectified Gaussian.
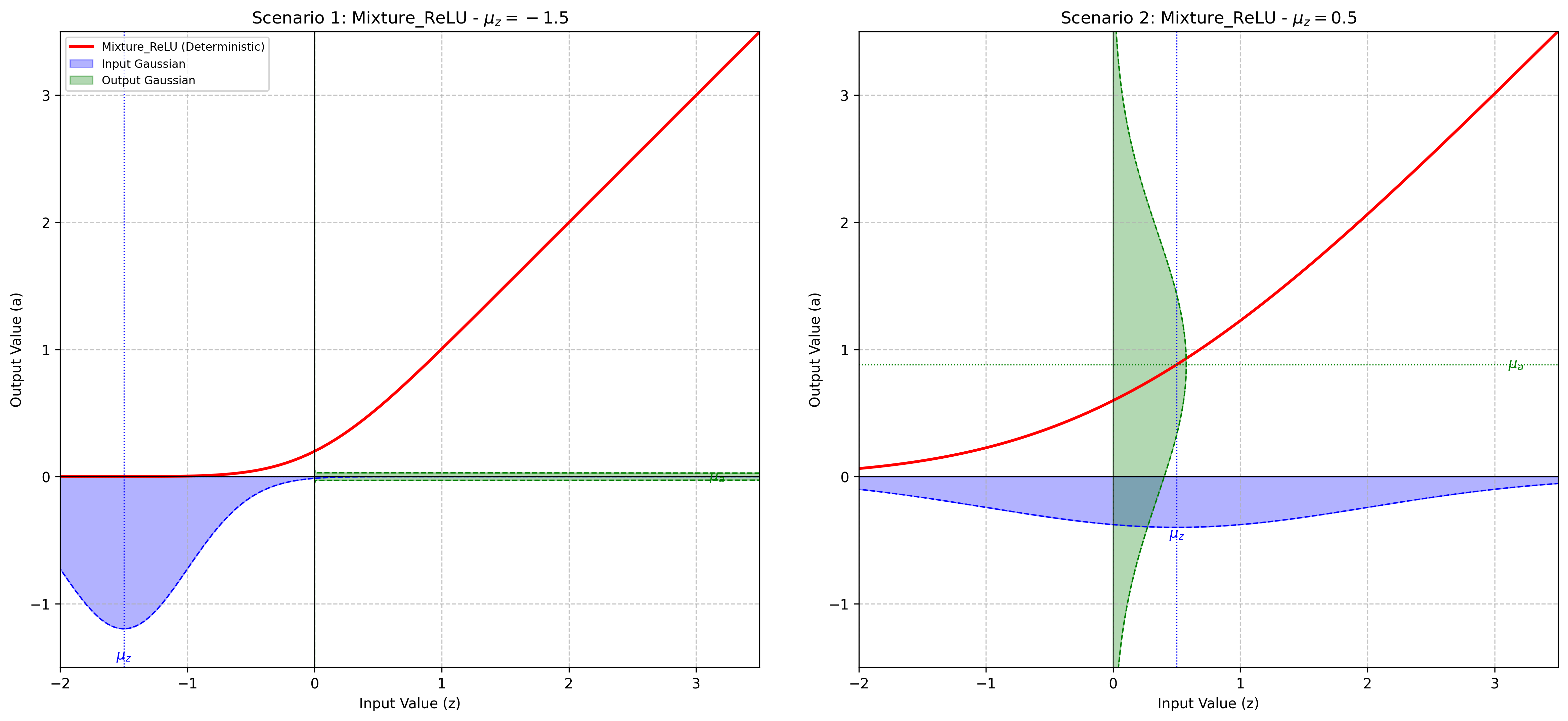
Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.MixtureSigmoid[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies a probabilistic picewise-linear Sigmoid-like function.
This layer processes an input Gaussian distribution and outputs the moments for a picewise-linear Sigmoid-like function. This layer relies on exact moment calculations.
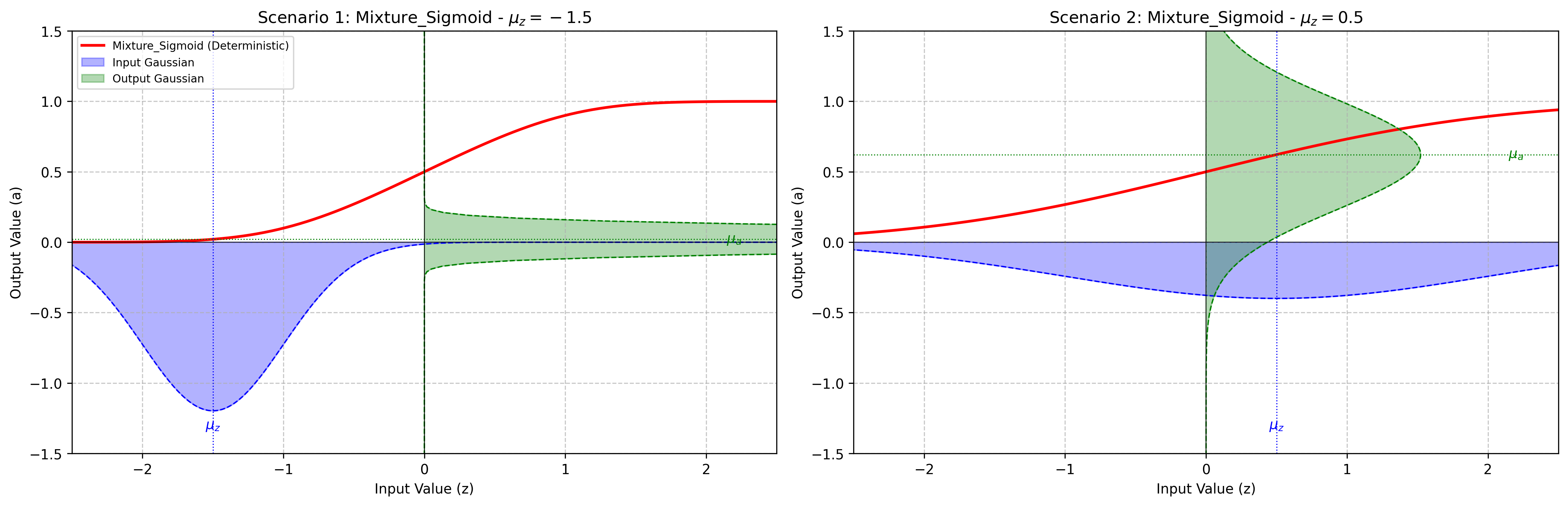
Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.MixtureTanh[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies a probabilistic piecewise-linear Hyperbolic Tangent function.
This layer processes an input Gaussian distribution and outputs the moments for a picewise-linear Tanh-like function. This layer relies on exact moment calculations.
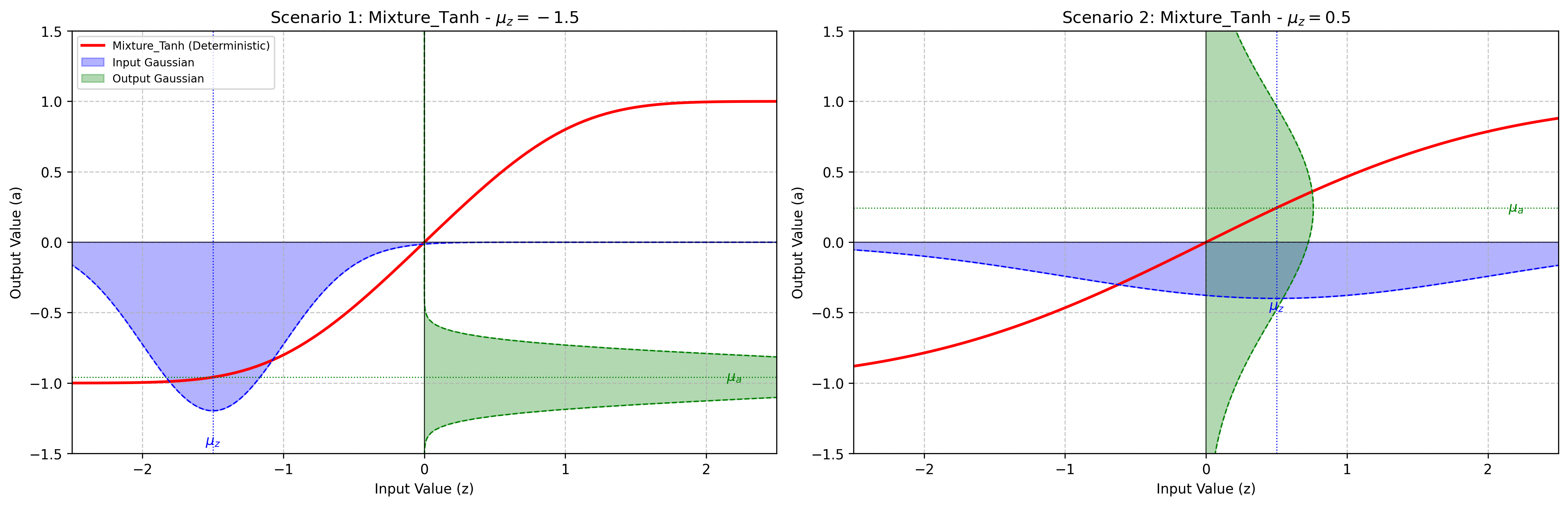
Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.Softplus[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies the Softplus function element-wise.
Softplus is a smooth approximation of the ReLU function. This layer relies on a first-order Taylor-series approximation where the activation function is locally linearized at the input expected value.
\[\text{Softplus}(x) = \log(1 + e^{x})\]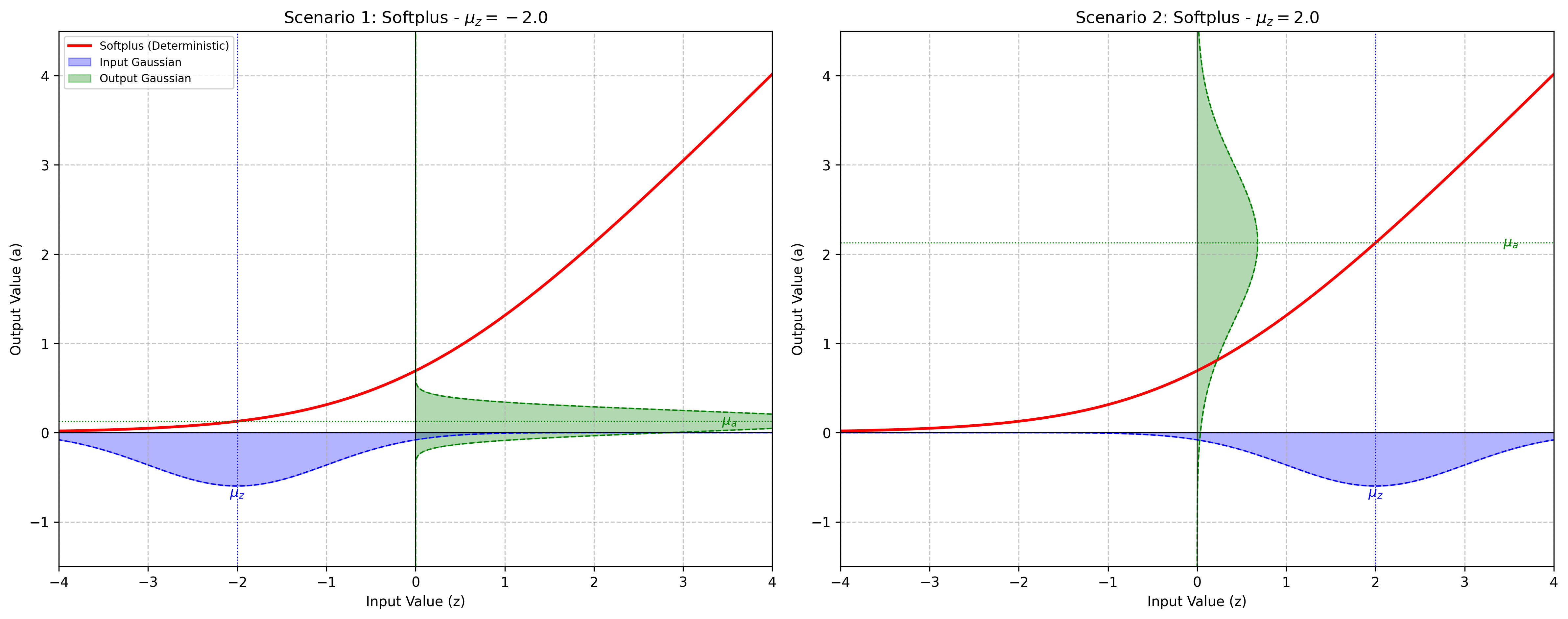
Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.LeakyReLU[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies the Leaky Rectified Linear Unit function element-wise.
This is a variant of ReLU that allows a small, non-zero gradient when the unit is not active. This layer relies on a first-order Taylor-series approximation where the activation function is locally linearized at the input expected value.
\[\begin{split}\text{LeakyReLU}(x) = \begin{cases} x & \text{if } x \geq 0 \\ \alpha x & \text{ otherwise } \end{cases}\end{split}\]Where \(\alpha\) is the negative_slope and is set to 0.1.
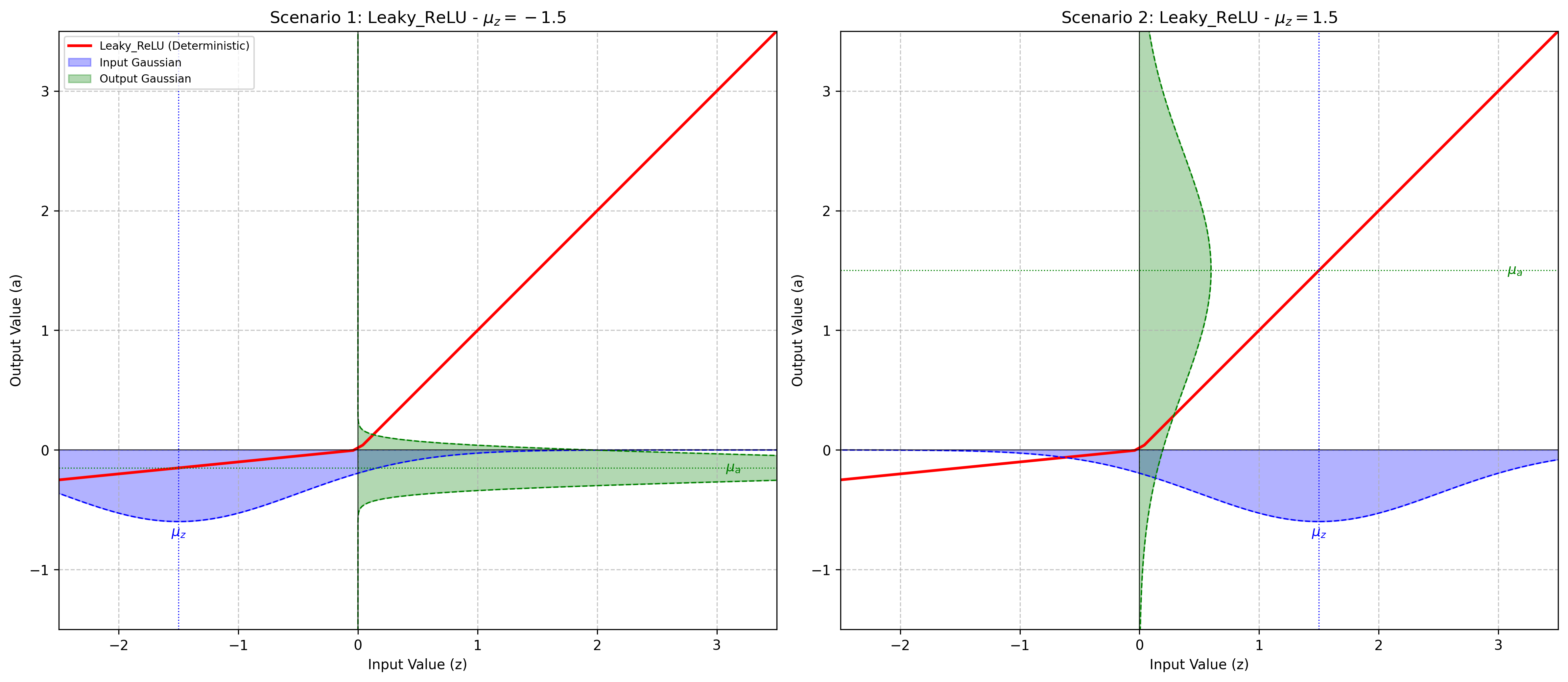
Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.Softmax[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies a Local-Linearization of the Softmax function to an n-dimensional input.
The Softmax function rescales the input so that the elements of the output lie in the range [0,1] and sum to 1. It is commonly used as the final activation function in a classification network to produce probability distributions over classes.
\[\text{Softmax}(x_{i}) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.EvenExp[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies the EvenExp activation function.
This function allows passing only the odd postions of the output layer through an exponential activation function. This is used for going from V2_bar to V2_bar_tilde for the aleatoric uncertainty inference in the case of heteroscedastic regression.
\[\begin{split}\text{EvenExp}(x) = \begin{cases} \exp(x) & \text{if } x \text{ is at an odd position}\\ x & \text{if } x \text{ is at an even position} \end{cases}\end{split}\]Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.Remax[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies a probabilistic Remax approximation function.
Remax is a softmax-like activation function which replaces the exponential function by a mixtureRelu. It rescales the input so that the elements of the output lie in the range [0,1] and sum to 1. It is commonly used as the final activation function in a classification network to produce probability distributions over classes.
\[\text{Remax}(x_{i}) = \frac{\text{ReLU}(x_i)}{\sum_j \text{ReLU}(x_j)}\]Initializes the BaseLayer with a C++ backend instance.
- class pytagi.nn.activation.ClosedFormSoftmax[source]#
Bases:
pytagi.nn.base_layer.BaseLayerApplies a probabilistic Softmax approximation function.
Closed-form softmax is an approximation of the deterministic softmax function that provides a closed-form solution for the output moments of Gaussian inputs. It is commonly used as the final activation function in a classification network to produce probability distributions over classes.
\[\text{Softmax}(x_{i}) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]Initializes the BaseLayer with a C++ backend instance.
